Se dice que una relación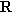 
sobre un conjunto A es una relación de orden parcial si esta es reflexiva,
antisimétrica o transitiva.
sobre un conjunto A es una relación de orden parcial si esta es reflexiva,
antisimétrica o transitiva.
Si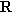
es un orden parcial sobre A, se utiliza la notación a 
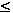b para indicar que (a, b)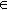 
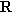. Esta notación
sugiere que estamos interpretando la relación como orden sobre los elementos.
es un orden parcial sobre A, se utiliza la notación a
b para indicar que (a, b)
. Esta notación
sugiere que estamos interpretando la relación como orden sobre los elementos.EJEMPLO:
Sea A={a, b, c, d, e} y sea
una relación sobre A definida como sigue: =
{(a, a), (a, b), (a, c), (a, d), (a, e), (b, b), (b, c), (b, e), (c, c), (c,
e), (d, d), (d, e), (e, e)}
Representada en la siguiente tabla:
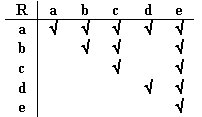
Como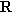
es reflexiva, antisimétrica y transitiva por lo tanto es una relación
de orden parcial.
es reflexiva, antisimétrica y transitiva por lo tanto es una relación
de orden parcial. Un conjunto A junto con un orden parcial
sobre A, es llamado un conjunto parcialmente ordenado y se deporta por (A,
). Un conjunto parcialmente ordenado es conocido como POSET (del inglés:
partially ordered set).EJEMPLO:
Sea A el conjunto de
y sea una relación
sobre A , tal que (a, b)
si a divide
a b (con residuo igual a cero).
Entonces como cualquier entero se divide a si mismo,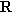
es una relación reflexiva. Si a divide a b significa que
b no divide a a, a menos que sea a = b, por lo que
es antisimétrica,
y puesto que si a divide a b y b divide a c entonces
a divide a c, por lo que
es transisitva. enconsecuencia
es un orden parcial.En realidad un conjunto parcialmente ordenado es denotado como (A, ).
es una relación reflexiva. Si a divide a b significa que
b no divide a a, a menos que sea a = b, por lo que
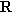es antisimétrica,
y puesto que si a divide a b y b divide a c entonces
a divide a c, por lo que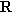
es transisitva. enconsecuencia
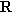es un orden parcial.En realidad un conjunto parcialmente ordenado es denotado como (A, 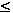).DEFINICIÓN:
Si
es un orden parcial
sobre A y si x, y
A y x y
y
x, se dice que x y y son comparables . Y si x, y
A y x 
y 
y
x, se dice que x y y son incomparables.DEFINICIÓN:
Una relación
sobre un conjunto A que es irreflexiva, simétrica y transitiva es llamada
de orden propia y se denota <.DEFINICIÓN:
Si cada par de elementos de A son comparables se dice que
es un orden total,
es decir, un orden parcial
es un orden total, (orden lineal ) si y solo si 
x,y,
x y
ó y
x es siempre verdadero.
En este caso (A, )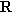
es un conjunto totalmente ordenado ó también llamado cadena (chain).
)
es un conjunto totalmente ordenado ó también llamado cadena (chain).EJEMPLO:
Los números naturales con la relación (
,
) y los números
enteros con la relación (,
) son ambos cadenas.
También el conjunto de las palabras del idioma español
con el orden lexicográfico es una cadena.
DEFINICION:
La longitud de una cadena es la cantidad de elementos de la misma .
DEFINICIÓN:
Si todos los elementos de un conjunto A son no comparables, entonces
se dice que es una anticadenas, es decir, un orden parcial
es una anticadena si
x, y
A, x 
y y
x.
En este caso (A, )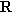
es una anticadena.
)
es una anticadena.EJEMPLO:
Sean A = {a, b, f, d, e} y sea
un orden parcial. Entonces (A,
)
es un conjunto parcialmente ordenado donde:{a, b, c, e} cadena
{a, b, c} cadena
{a, d, e} cadena
{a} cadena
{b, d} anticadena
{c, d} anticadena
Representemos a R por medio de una tabla.
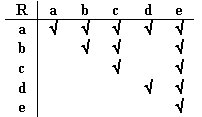
0 comentarios for "RELACION DE ORDEN PARCIAL"
Publicar un comentario