PRODUCTO CARTESIANO:
Antes de afrontar el estudio de las relaciones binarias, veamos algunos conceptos que es necesario conocer:
Producto cartesiano:
Definimos los conjuntos:

Obtenemos el producto cartesiano de A por B, colocando en una tabla los elementos del conjunto A en el eje horizontal y los de B en vertical, en la intersección colocamos los pares ordenados correspondientes, percatarse que en el par ordenado, en primer lugar se coloca el elemento de A, del eje horizontal y en segundo lugar el de B, del eje vertical.
La enumeración de los elementos, del conjunto de pares ordenados, seria el siguiente:

PAR ORDENADO:Las partes de un par ordenado son:- Primer conjunto
- Primer componente
- Segundo conjunto
- Segundo componente
Del siguiente par ordenado (a, b) podemos decir que:
- a es el primer componente del primer conjunto y;
- b como el segundo componente del segundo conjunto.
Matemáticamente esto se expresa:
Y se lee: El producto de A con B, es el conjunto de los pares ordenados (x,y) tales que x pertenece a A e y pertenece a B.
DOMINIO:
El dominio de definición de una función f:X→Y se define como el conjuto X de todos los elementos x para los cuales la función f asocia algún y perteneciente al conjunto Y de llegada, llamado codominio. Esto, escrito de manera formal:
EJEMPLOS:
Algunos dominios de funciones reales de variable real:
 El dominio de esta función, así como el de cualquier funcion polinomica y exponencial, es
El dominio de esta función, así como el de cualquier funcion polinomica y exponencial, es  .
.
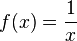 El dominio de esta función es
El dominio de esta función es  puesto que la función no esta definida para x = 0.
puesto que la función no esta definida para x = 0.
 El dominio de esta función es
El dominio de esta función es  ya que los logaritmos están definidos sólo para números positivos.
ya que los logaritmos están definidos sólo para números positivos.
-
 El dominio de esta función es
El dominio de esta función es 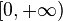 porque la raíz de un número negativo no existe en el cuerpo de los reales
porque la raíz de un número negativo no existe en el cuerpo de los reales
RANGO:
Se denomina rango estadístico (R) o recorrido estadístico al intervalo entre el valor máximo y el valor mínimo; por ello, comparte unidades con los datos. Permite obtener una idea de la dispersión de los datos, cuanto mayor es el rango, más dispersos están los datos de un conjunto.
Por ejemplo, para una serie de datos de carácter cuantitativo, como lo es la estatura medida en centímetros, tendríamos:
es posible ordenar los datos como sigue:
donde la notación x(i) indica que se trata delelemento i-ésimo de la serie de datos. De este modo, el rango sería la diferencia entre el valor máximo (k) y el mínimo; o, lo que es lo mismo:
En nuestro ejemplo, con cinco valores, nos da que R = 185-155 = 30.





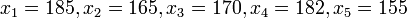

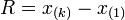


0 comentarios for "CONCEPTOS PREVIOS"
Publicar un comentario