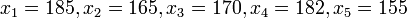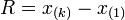Relaciones Binarias

Una relación, de los conjuntos es un subconjunto del producto cartesiano, Una relación binaria es una relación entre dos conjuntos.El concepto de relación implica la idea de enumeración, de algunos de los elementos, de los conjuntos que forman tuplas.

Un caso particular es cuando todos los conjuntos de la relación son iguales,en este caso se representa como , pudiéndose decir que la relación pertenece a A a la n.

Definición matemática de Relación:

En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamado Recorrido o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.

Producto cartesiano:

El producto cartesiano de dos conjuntos A y B es el conjunto de todos los pares ordenados (x, y) donde x∈A e y ∈ B.

En símbolos, A x B = {(x, y) / x∈A ∧ y ∈ B }

Por lo tanto : (x, y) ∈ A x B si y sólo si x∈A ∧ y ∈ B

Ejemplo:

Sean los conjuntos A={1,2,3} y B={4,5,6} se tiene:

A x B={(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5) ,(3,6)}

El producto cartesiano A x B no es igual al producto cartesiano B x A (no es conmutativo)

PROPIEDADES DE LA RELACION:

En matemáticas, una relación binaria es una relación matemática R entre los elementos de dos conjuntos A y B. Una relación de este tipo se puede representar mediante pares ordenados,:
También puede expresarse: Una relación binaria puede tener ciertas propiedades, según los pares ordenados que formen parte de dicha relación o no formen parte de ella, veamos algunas:

Propiedad reflexiva:

Una relación tiene la propiedad reflexiva, si todo elemento esta relacionado consigo mismo, si no todos los elementos del conjunto están relacionados consigo mismo se dice que la relación no es reflexiva.

Para todo elemento a que pertenezca al conjunto A, el par ordenado (a,a) pertenece a la relación binaria R.

Téngase en cuenta que debe cumplirse para todos los elementos del conjunto sin excepción, si esta propiedad solo se da en algunos casos la relación no es reflexiva: Se escribe a R a ∀a∈A.

Ejemplo:

1) En N la relación R definida por: “x R y ⇔ x divide a y”
es reflexiva ya que ∀x∈N, x R x porque x divide a x

2) En N la relación R definida por:
“a R b ⇔ a es el doble de b”.
no es reflexiva ya que (1, 1) ∉R puesto que 1 no es el doble de 1

Si la relación R es reflexiva entonces la diagonal pertenece a la relación.

No existe ningún elemento a en A, para el que el par ordenado (a,a) no pertenezca a la relación R. Puede verse que estas dos afirmaciones son iguales.

Teorema: Una relación R en un conjunto es reflexiva si y solo si la diagonal principal de la matriz asociada a la relación tiene únicamente unos. De la misma forma es Irreflexiva si tiene solamente ceros.

Propiedad irreflexiva:

Una relación binaria tiene la propiedad irreflexiva, también llamada: antirreflexiva o antirrefleja, si ningún elemento del conjunto esta relacionado consigo mismo:

No existe ningún elemento a en el conjunto A que cumpla que: (a,a) pertenezca a R.

Propiedad simétrica:

No es transitiva ya que (4, 2) Î R y (2, 1) Î R puesto que 4 es el doble de 2 y 2 es el doble de 1, sin embargo 4 no es el doble de 1, de donde (4,1)Ï R

Propiedad R	Se satisface sii	No se satisface sii
Reflexiva	"aÎA a R a	$ aÎA (a,a)ÏR
Simétrica	" a, b ÎA: a R b Þ b R a	$ a, b ÎA: (a, b) Î R Ù (b, a) Ï R
Antisimétrica	" a, b ÎA: [a R b Ù b R a] Þ a = b	$ a, b ÎA: (a, b) Î R Ù (b, a) Î R Ù a ¹ b
Transitiva	" a, b, c ÎA: [a R b Ù b R c] Þ a R c	$ a, b, c ÎA: (a, b) Î R Ù (b, c) Î R Ù (a, c) Ï R

Relación inversa:

Una relación binaria tiene la propiedad simétrica, si se cumple que un par ordenado (a,b) pertenece a la relación entonces el par (b,a) también pertenece a esa relación, Si cuando un elemento esta relacionado con un segundo elemento, el segundo también se relaciona con el primero, con símbolos: (x ,y) ∈ R ⇒ (y ,x) ∈ R :

Para todo par ordenado (a,b) que pertenezca a R, implica que el par (b,a) también pertenece a R, téngase en cuenta que si el par (a,b) no pertenece a la relación el par (b,a) tampoco tiene que pertenecer a esa relación:

Teorema: Una relación R es simétrica si y solo si los elementos opuestos con respecto a la diagonal principal son iguales.

si ∀ a, b ∈A: a R b ⇒ b R a

Ejemplo:

1) En Z la relación R definida por: “a R b ⇔ a – b es múltiplo de 2”.

es simétrica ya que si a R b ⇒ hay p∈Z tal que a – b = 2p ⇒ b – a = 2(-p) con -p ∈ Z ⇒ b R a

2) En N la relación R definida por: “x R y ⇔ x divide a y” no es simétrica ya que 2 R 4 porque 2 divide a 4 pero 4 no divide a 2 por lo tanto (4,2) ∉R

Si la relación R es simétrica sobre A entonces los pares relacionados se reflejan respecto a la diagonal principal.

Teorema: Una relación R en conjunto es Antisimétrica si y solo si los elementos opuestos con respeto a la diagonal principal no pueden ser iguales a 1; esto es, puede aparecer 0 con 1 o pueden aparecer ceros.

Antisimétrica:

Si cuando un elemento esta relacionado con un segundo elemento diferente, el segundo no se relaciona con el primero, con símbolos: ∀x, y, ((x, y) ∈ R ∧ (y, x) ∈ R → x = y) La antisimetría no es lo

si ∀ a, b ∈A: [a R b ∧ b R a] ⇒ a = b

Otra manera de expresarlo:

Si a≠b ⇒ [ (a,b) ∉ R ∨ (b,a) ∉ R ]

Ejemplo:

1) En N la relación R definida por: “x R y ⇔ x divide a y” es antisimétrica

Ya que si a R b y b R a entonces existen n, m ∈N tales que:

b = an y a = bm. Combinándolas, a = bm = (a.n).m ⇒ n.m = 1 ⇒

n = m = 1 ⇒ a = b.

2) En Z la relación R definida por: “a R b ⇔ a – b es múltiplo de 2”.

no es antisimétrica ya que 2R4 y 4R2, pero 2≠4

Si la relación R es antisimétrica pueden existir pares por encima o por debajo de la diagonal pero ningún par tiene reflejo respecto a la diagonal principal excepto la diagonal misma.

Transitiva:

Si cuando un elemento esta relacionado con un segundo elemento y el segundo esta relacionado con un tercero, entonces el primero está relacionado con el tercero:

1) En N la relación R definida por: “x R y Û x divide a y”

es transitiva ya que si a R b y b R c entonces existen n, m ÎN tales que:

b = an y c = bm. Combinándolas, c = bm = (a.n).m= a(n.m) con n.m ÎN Þ b R c.

2) En N la relación R definida por: “a R b Û a es el doble de b”.

La relación R es transitiva si cada vez que hay un camino entre tres elementos, también está la flecha que comienza en el principio del camino y va al elemento que es final del camino.

Asimetrica:

Una relación R en un conjunto A es asimétrica si cuando a R b, entonces b Ra. De esto se sigue que R no es simétrica si se tiene a y b e A con ambos a R b y b R a.

Opuesto de la simetría.

Ejemplo para todas las relaciones

Cuando tenemos la matriz de una relación es muy fácil verificar si es reflexiva, Irreflexiva, Simétrica, Asimétrica, Antisimétrica, Transitiva:

Ejemplo.- Sea A = { a, b, c, d, e }

R1 = { (a,a), (b,b), (a,c), (b,c), (c,a), (d,d) }

R2 = { (a,a), (a,d), (c,b), (d,a), (c,e), (e,e) }

R3 = { (a,a), (b,b), (c,c), (d,d), (e,e), (b,c), (b,a) }

R4 = { (a,a), (a,b), (b,a), (b,b), (b,c), (b,e), (c,e), (b,d), (d,a), (e,e) }

R5 = { (a,c), (a,e), (e,c), (b,c) }

R6 = { ( (a,a), (b,b), (c,c), (d,d), (e,e), (a,e), (b,c), (c,b), (e,a) }

R7 = { (a,b), (b,d), (c,a), (d,e), (e,c), (b,c), (b,a) }

Sea R una relación. Definimos la relación inversa de R y la notamos R -1 , al conjunto con la siguiente propiedad:

Se llama relación inversa a la relación que resulta de cambiar el orden de los
conjuntos A x B por B x A
La relación inversa la designaremos por R −1

Ejemplo:

Sea R la relación definida por: G = {(a,1),(a,2),(b,3),(c,5)}

La relación inversa G-1 será: G-1= {(1,a),(2,a),(3,b),(5,c)}

Existe una relación inversa entre la suma y la resta

Si consideramos un hecho matemático, por ejemplo

3 + 7 = 10. Entonces los siguientes también son verdaderos:

10 - 3 = 7

10 - 7 = 3

Existen relaciones similares para la resta, por ejemplo:

10 – 3 = 7. Entonces las siguientes también son verdaderas:

3 + 7 = 10

7 + 3 = 10

La razón de esto es porque nos encontramos frente a una ecuación. Una ecuación es balanceada o igual a ambos lados del signo igual (=). Si se hace exactamente lo mismo a ambos lados de la ecuación, seguirá siendo balanceada o igual.

En el ejemplo anterior comenzamos con la ecuación 3 + 7 = 10

Resta el mismo número de ambos lados 3 + 7 - 3 = 10 - 3

En el lado izquierdo 3 – 3 resultan 0, lo que nos deja 7 = 10 – 3

Invierte los términos de la ecuación para presentarla de una manera más normal 10 – 3 = 7

Hay una relación inversa entre la multiplicación y la división.

La ecuación 45 ÷ 5 = 9 tiene las siguientes relaciones inversas:

5 * 9 = 45

9 * 5 = 45

Existen relaciones similares para la multiplicación. La ecuación 3 * 7 = 21 tiene las siguientes relaciones:

21 ÷ 3 = 7

21 ÷ 7 = 3

Relación compuesta.

Sean R, S relaciones. Definimos “la relación compuesta de S y R” y la notamos , al conjunto con la siguiente propiedad:

Se dice que en A se ha definido una ley de composición interna u operación
cuando se define una Función del producto cartesiano A x A en A de tal forma que
el par de elementos (a, b) genere otro elemento c, tal que c también pertenece al
conjunto A.

Para representar el elemento imagen del par (a, b) se utiliza la notación c = a f b
donde f es cualquier símbolo. Por ejemplo ⋅ , ⊥ , ∗ , Θ , ° , ◊ , ∇

Se dice que en A se a definido una ley de composición externa sobre el conjunto B

cuando se define una Función del producto cartesiano BXA en A

Es una "generalización" de la composición de funciones. Básicamete es así:

aRb y bSc implican que aSRc

donde SR es la "composición" de las relaciones R y S en este orden.

Si lo quieres ver en notación de conjuntos sería así:

(a,b)∈R y (b,c)∈S implican que (a,c)∈ S·R

Relación de orden
Diremos que una relación binaria sobre A, es una relación de orden parcial si

satisface las tres propiedades:
‰ R es reflexiva
‰ R es antisimétrica
‰ R es transitiva
En este caso diremos que el conjunto A está parcialmente ordenado

Ejemplo:

1) En D60 , el conjunto de todos los divisores de 60, la relación R definida por:
a R b ⇔ a divide a b.
2) En R, la relación definida por a R b ⇔ a ≤ b.
Demuestra que estas son relaciones de orden.

Diremos que una relación binaria R sobre A, es una relación de orden total si es
una relación de orden parcial y además se satisface que:

∀ a, b ∈A: [a R b ∨ b R a]

En este caso diremos que el conjunto A está totalmente ordenado

Mariangel Aparicio

21:08

0 Respuestas

PRODUCTO CARTESIANO:

Antes de afrontar el estudio de las relaciones binarias, veamos algunos conceptos que es necesario conocer:

Producto cartesiano:

Definimos los conjuntos:

A = \{1, 4, 6 \} \,

B = \{2, 3, 5 \} \,

\begin{array}{|r|ccc|} \hline 5 & (1,5) & (4,5) & (6,5) \\ 3 & (1,3) & (4,3) & (6,3) \\ 2 & (1,2) & (4,2) & (6,2) \\ \hline A \times B & 1 & 4 & 6 \\ \hline \end{array}

Obtenemos el producto cartesiano de A por B, colocando en una tabla los elementos del conjunto A en el eje horizontal y los de B en vertical, en la intersección colocamos los pares ordenados correspondientes, percatarse que en el par ordenado, en primer lugar se coloca el elemento de A, del eje horizontal y en segundo lugar el de B, del eje vertical.

La enumeración de los elementos, del conjunto de pares ordenados, seria el siguiente:

A \times B = \{ (1,2), (1,3), (1,5), (4,2), (4,3), (4,5), (6,2), (6,3), (6,5) \} \,

PAR ORDENADO:Las partes de un par ordenado son:

Primer conjunto

Primer componente

Segundo conjunto

Segundo componente

Del siguiente par ordenado (a, b) podemos decir que:

a es el primer componente del primer conjunto y;

b como el segundo componente del segundo conjunto.

Matemáticamente esto se expresa:

A \times B = \{(x,y) \; | \quad x \in A \quad \land \quad y \in B \}

Y se lee: El producto de A con B, es el conjunto de los pares ordenados (x,y) tales que x pertenece a A e y pertenece a B.

DOMINIO:

El dominio de definición de una función f:X→Y se define como el conjuto X de todos los elementos x para los cuales la función f asocia algún y perteneciente al conjunto Y de llegada, llamado codominio. Esto, escrito de manera formal:

$D_f = \; \left\{x \in X | \exists y \in Y: f(x)=y\right\}$

EJEMPLOS:

Algunos dominios de funciones reales de variable real:

$f(x)=x^2 \,\!$ El dominio de esta función, así como el de cualquier funcion polinomica y exponencial, es $\mathbb{R}$ .

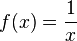$f(x)= \frac{1}{x}$ El dominio de esta función es $\mathbb{R}-\lbrace0\rbrace$ puesto que la función no esta definida para x = 0.

$f(x)= \log(x) \,\!$ El dominio de esta función es $(0,{+}\infty)$ ya que los logaritmos están definidos sólo para números positivos.

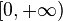$f(x)= \sqrt{x}$ El dominio de esta función es $\lbrack0,{+}\infty)$ porque la raíz de un número negativo no existe en el cuerpo de los reales

RANGO:

Se denomina rango estadístico (R) o recorrido estadístico al intervalo entre el valor máximo y el valor mínimo; por ello, comparte unidades con los datos. Permite obtener una idea de la dispersión de los datos, cuanto mayor es el rango, más dispersos están los datos de un conjunto.

Por ejemplo, para una serie de datos de carácter cuantitativo, como lo es la estatura medida en centímetros, tendríamos:

x_1=185, x_2=165, x_3=170, x_4=182, x_5=155

es posible ordenar los datos como sigue:

x_{(1)}=155, x_{(2)}=165, x_{(3)}=170, x_{(4)}=182, x_{(5)}=185

donde la notación x_(i) indica que se trata delelemento i-ésimo de la serie de datos. De este modo, el rango sería la diferencia entre el valor máximo (k) y el mínimo; o, lo que es lo mismo: